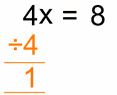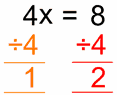INDICES

Indices & the Law of Indices

Introduction

Indices are a useful way of more simply expressing large numbers. They also present us with many useful properties for manipulating them using what are called the Law of Indices.

What are Indices?

The expression 2⁵ is defined as follows:

We call "2" the base and "5" the index.

Law of Indices

To manipulate expressions, we can consider using the Law of Indices. These laws only apply to expressions with the same base, for example, 3⁴ and 3² can be manipulated using the Law of Indices, but we cannot use the Law of Indices to manipulate the expressions 3⁵ and 5⁷ as their base differs (their bases are 3 and 5, respectively).

Here are the examples:

Simplify 2⁰:

Simplify 2^-2:

Simplify : (note: 5 = 5¹)

Simplify

:

Simplify (y²)⁶:

Simplify 125^2/3:

ALGEBRA

Algebra 

is one of the broad parts of mathematics, together with number theory, geometry and analysis. In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics.

Algebra began with computations similar to those of arithmetic, with letters standing for numbers.^[8] This allowed proofs of properties that are true no matter which numbers are involved. For example, in the quadratic equation:

${\displaystyle ax^{2}+bx+c=0,}$

${\displaystyle a,b,c}$ can be any numbers whatsoever (except that ${\displaystyle a}$ cannot be ${\displaystyle 0}$), and the quadratic formula can be used to quickly and easily find the value of the unknown quantity ${\displaystyle x}$.

As it developed, algebra was extended to other non-numerical objects, such as vectors, matrices, and polynomial. Then the structural properties of these non-numerical objects were abstracted to define algebraic structures such as groups, rings, and fields.

How to Solve

Instead of saying "obviously x=2", use this neat step-by-step approach:

• Work out what to remove to get "x = ..."
• Remove it by doing the opposite
• Do that to both sides

And what is the opposite of multiplying? Dividing!

Have a look at this example:

We want to remove the "4"	To remove it, do the opposite, in this case divide by 4:	Do it to both sides:	Which is ...	Solved!

Permutations

There are basically two types of permutation:

1. Repetition is Allowed: such as the lock above. It could be "333".
2. No Repetition: for example the first three people in a running race. You can't be first and second.

1. Permutations with Repetition

These are the easiest to calculate.

When we have n things to choose from ... we have n choices each time!

When choosing r of them, the permutations are:

n × n × ... (r times)

(In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time.)

Which is easier to write down using an exponent of r:

n × n × ... (r times) = n^r

Example: in the lock above, there are 10 numbers to choose from (0,1,...9) and we choose 3 of them:

10 × 10 × ... (3 times) = 10³ = 1,000 permutations

So, the formula is simply:

nr

where n is the number of things to choose from, and we choose r of them (Repetition allowed, order matters)

2. Permutations without Repetition

In this case, we have to reduce the number of available choices each time.

For example, what order could 16 pool balls be in?

After choosing, say, number "14" we can't choose it again.

So, our first choice has 16 possibilites, and our next choice has 15 possibilities, then 14, 13, etc. And the total permutations are:

16 × 15 × 14 × 13 × ... = 20,922,789,888,000

But maybe we don't want to choose them all, just 3 of them, so that is only:

16 × 15 × 14 = 3,360

In other words, there are 3,360 different ways that 3 pool balls could be arranged out of 16 balls.

Without repetition our choices get reduced each time.

But how do we write that mathematically? Answer: we use the "factorial function"

	The factorial function (symbol: !) just means to multiply a series of descending natural numbers. Examples: 4! = 4 × 3 × 2 × 1 = 24 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5,040 1! = 1
Note: it is generally agreed that 0! = 1. It may seem funny that multiplying no numbers together gets us 1, but it helps simplify a lot of equations.

So, when we want to select all of the billiard balls the permutations are:

16! = 20,922,789,888,000

But when we want to select just 3 we don't want to multiply after 14. How do we do that? There is a neat trick ... we divide by 13! ...

16 × 15 × 14 × 13 × 12 ...		= 16 × 15 × 14 = 3,360
13 × 12 ...

Do you see? 16! / 13! = 16 × 15 × 14

The formula is written:

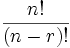where n is the number of things to choose from, and we choose r of them (No repetition, order matters)

Examples:

Our "order of 3 out of 16 pool balls example" is:

16!	=	16!	=	20,922,789,888,000	= 3,360
(16-3)!		13!		6,227,020,800

(which is just the same as: 16 × 15 × 14 = 3,360)

How many ways can first and second place be awarded to 10 people?

10!	=	10!	=	3,628,800	= 90
(10-2)!		8!		40,320

(which is just the same as: 10 × 9 = 90)

Combination

In English we use the word "combination", without thinking if the order of things is important. In other words:

	"My veggie salad is a combination of lettuce, spinach and broccoli" We don't care what order the veggies are in, they could also be "lettuce, spinach and broccoli" or "broccoli, lettuce and spinach", its the same veggie salad.
	"The combination to the locker is 108". Now we do/must care about the order. "801" won't work, nor will "810". It has to be exactly 1-0-8.

Whereas, in Mathematics we use more precise language:

	If the order doesn't matter, it is a Combination.
	If the order does matter, it is a Permutation.

So, we should really call this a "Permutation Lock"!

In other words:

A Permutation is an ordered Combination.