There are basically two types of permutation:
- Repetition is Allowed: such as the lock above. It could be "333".
- No Repetition: for example the first three people in a running race. You can't be first and second.
1. Permutations with Repetition
These are the easiest to calculate.
When we have n things to choose from ... we have n choices each time!
When choosing r of them, the permutations are:
n × n × ... (r times)
(In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time.)
Which is easier to write down using an exponent of r:
n × n × ... (r times) = nr
Example: in the lock above, there are 10 numbers to choose from (0,1,...9) and we choose 3 of them:
10 × 10 × ... (3 times) = 103 = 1,000 permutations
So, the formula is simply:
| nr |
where n is the number of things to choose from, and we choose r of them
(Repetition allowed, order matters) |
2. Permutations without Repetition
In this case, we have to reduce the number of available choices each time.
For example, what order could 16 pool balls be in?
After choosing, say, number "14" we can't choose it again.
So, our first choice has 16 possibilites, and our next choice has 15 possibilities, then 14, 13, etc. And the total permutations are:
16 × 15 × 14 × 13 × ... = 20,922,789,888,000
But maybe we don't want to choose them all, just 3 of them, so that is only:
16 × 15 × 14 = 3,360
In other words, there are 3,360 different ways that 3 pool balls could be arranged out of 16 balls.
Without repetition our choices get reduced each time.
But how do we write that mathematically? Answer: we use the "factorial function"
|
The factorial function (symbol: !) just means to multiply a series of descending natural numbers. Examples:
- 4! = 4 × 3 × 2 × 1 = 24
- 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5,040
- 1! = 1
|
| Note: it is generally agreed that 0! = 1. It may seem funny that multiplying no numbers together gets us 1, but it helps simplify a lot of equations. |
So, when we want to select all of the billiard balls the permutations are:
16! = 20,922,789,888,000
But when we want to select just 3 we don't want to multiply after 14. How do we do that? There is a neat trick ... we divide by 13! ...
16 × 15 × 14 × 13 × 12 ...
| | = 16 × 15 × 14 = 3,360 |
13 × 12 ...
| |
Do you see? 16! / 13! = 16 × 15 × 14
The formula is written:
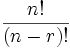 |
where n is the number of things to choose from, and we choose r of them
(No repetition, order matters) |
Examples:
Our "order of 3 out of 16 pool balls example" is:
| 16! | = | 16! | = | 20,922,789,888,000 | = 3,360 |
| (16-3)! | 13! | 6,227,020,800 |
(which is just the same as: 16 × 15 × 14 = 3,360)
How many ways can first and second place be awarded to 10 people?
| 10! | = | 10! | = | 3,628,800 | = 90 |
| (10-2)! | 8! | 40,320 |
(which is just the same as: 10 × 9 = 90)
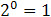 Simplify 2-2:
Simplify 2-2:
 Simplify
Simplify 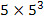 : (note: 5 = 51)
: (note: 5 = 51)



 can be any numbers whatsoever (except that
can be any numbers whatsoever (except that  cannot be
cannot be  ), and the quadratic formula can be used to quickly and easily find the value of the unknown quantity
), and the quadratic formula can be used to quickly and easily find the value of the unknown quantity  .
.